Crypto Journal Part III : Fully Homomorphic Encryption Part I : Secret Key Homomorphic Encryption Over Integers

Gentry's breakthrough results in simpler terms

EP

In the previous post we discussed homomorphic encryption in it’s most abstract terms we presented Paillier as a partially homomorphic encryption . Thank you @mortendahlcs for making a clarification about the terms described :

Alrighty then in this post I will try to explain an analogy between FHE and mathematics , and I will explain Gentry’s breakthrough by using a scheme published after his first papers where instead of using ideal lattices the scheme uses integers it will be easier to explain that way and also provide examples without much math .

In the next post we discuss Public Key HE and explain bootstrapping

We will start with some math this way we can have an abstraction of the subject and help us understand a bit more about homomorphic encryption in general .

Pre definitions

Gentry’s Fully Homomorphic Scheme

Craig Gentry released the first fully homomorphic encryption scheme that is based on ideal lattices ( no need to know what it is for now ) on June 25st 2009 . His scheme was constructed from a SHE scheme ( add & mul for limited number of times ) or in math words limited to evaluating low degree polynomials , limited here means that each ciphertext has some noise S in it and as you add and multiply ciphers the noise makes the end result indecipherable . He introduced bootstrapping which means that the scheme can evaluate it’s own decryption circuit and this property can make the scheme fully homomorphic bootstrapping refreshes the ciphertext by reducing the noise in each operation .

The scheme was considered secure but impractical because the bigger the security parameter the more computationally intensive was to compute the ciphers and their sizes were getting bigger .

Later on , Gentry, Marten van Dijk,Shai Halevi et al released a scheme based on the ideas that Gentry introduced ( bootstrapping ) but this time the scheme used integers instead of ideal lattices . The lattice scheme is incredibly complex , the integer one is simpler to explain especially the bootstrapping part so we will only discuss the latter .

SHE over Integers

Let’s restate that Gentry’s breaktrough was taking a somewhat fully homomorphic scheme and making fully homomorphic using bootstrapping so the scheme we are going to discuss now is somewhat homomorphic and we will use it to explain bootstrapping in more details.

Secret Key Scheme

In cryptography we generally ( I think ) talk about two different ways to do encyption either using a secret key , i.e same key is used to encrypt and decrypto , or public key where on key remains private (private key) used to decrypt and a key is public (public key) used to encrypt .

RSA for example is a public key scheme each user gets two keys let’s take Alice and Bob for a ride :

** You get the point **

Let’s describe the secret-key homomorphic scheme now .

** As we discussed above a scheme needs three algorithms KeyGen, Encrypt, Decrypt :

SCHEME HOMOMORPHISM

Let’s verify the scheme’s homomorphism :

Intuitive Application and Code

As you may have noticed the algorithm is designed to encrypt bits {0,1} so you may ask how do I sum 2 numbers ? Well as you may remember we discussed circuits before and here we can see them in action .

Adding binary numbers or just digits is done using an adder . An adder sums two binary digits and outputs their sum and the carry

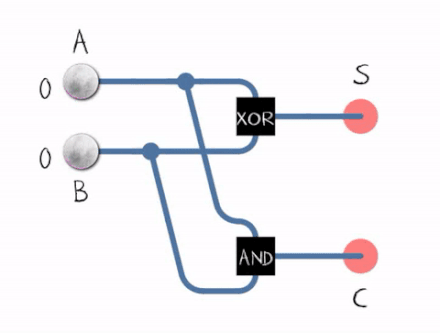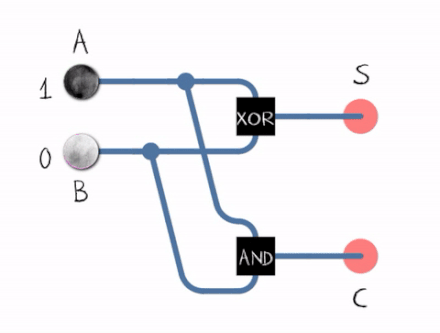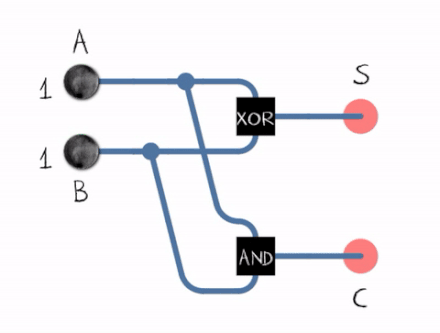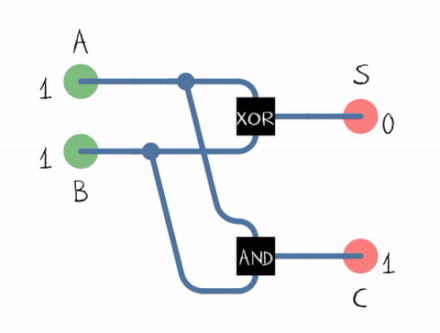
half_adder

From the gif above we can see that to construct a Half Adder we need a XOR Gate and an AND Gate , the XOR Gate outputs the sum of two bits and the AND Gate outputs the carryout .

There’s also what we call a full adder :

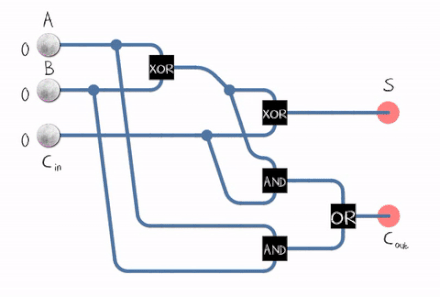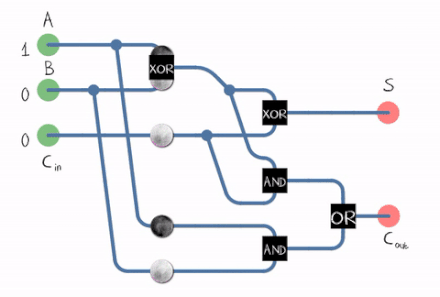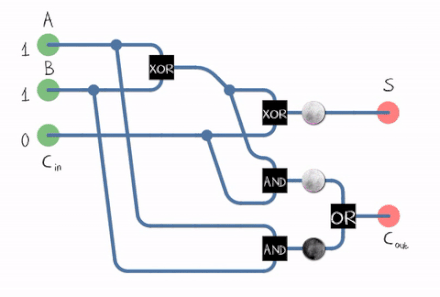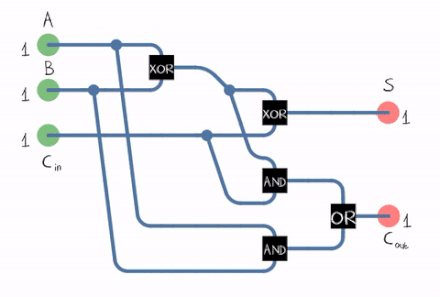
full_adder

A Full Adder can be constructed using two Half Adders and an OR Gate .

Now we have our circuits let’s move on two a practical example :

The following example builds functions to add two 4 Bit numbers from {0000,1111}


import sys
from random import randint

def tobits(val):
    l = [0]*(8)

    l[0]=val & 0x1
    l[1]=(val & 0x2)>>1
    l[2]=(val & 0x4)>>2
    l[3]=(val & 0x8)>>3
    return l

def XOR(a,b):
    return ( (NOT(a)*b) + (a*NOT(b)))

def NOT(val):
    return(val ^ 1)

def AND(a,b):
    return(a*b)

def OR(a,b):
    return(a+b)

def HA(bit1,bit2):
    sum=XOR(bit1,bit2)
    carryout=AND(bit1,bit2)
    return sum,carryout

def FA(bit1,bit2,cin):
    sum1,c1=HA(bit1,bit2)
    sum,c2=HA(sum1,cin)
    carryout=OR(c1,c2)
    return sum,carryout



def encrypt(bit,p):
    #q=randint(50000, 90000)    
    #r=randint(1,200)
    q = 2
    r = 0
    return(  q * p + 2*r +int(bit)),q,r

def decrypt(cipher,p):
    return (cipher % p) % 2

## values to test using same example as before

val1=10
val2=13

v1=[]
v2=[]

v1=tobits(val1)
v2=tobits(val2)

cin=0

#p =randint(3e23, 6e23)*2+1
p = 17
c_carryin,q,r=encrypt(cin,p)

print(v1)
print(v2)

#Cval(i)b(j) means Cipher i Bit j
cval1b0,q,r=encrypt(v1[0],p)
cval2b0,q,r=encrypt(v2[0],p)

cval1b1,q,r=encrypt(v1[1],p)
cval2b1,q,r=encrypt(v2[1],p)

cval1b2,q,r=encrypt(v1[2],p)
cval2b2,q,r=encrypt(v2[2],p)

cval1b3,q,r=encrypt(v1[3],p)
cval2b3,q,r=encrypt(v2[3],p)

"""At this point we have two ciphertext cval1,cval2 to do the sum we use a FA"""


## Addition between two bit arrays 
print("1 ",c_carryin)
c_sum1,c_carryout=FA(cval1b0,cval2b0,c_carryin )
c_sum2,c_carryout=FA(cval1b1,cval2b1,c_carryout )
c_sum3,c_carryout=FA(cval1b2,cval2b2,c_carryout )
c_sum4,c_carryout=FA(cval1b3,cval2b3,c_carryout )



sum1 = decrypt(c_sum1,p)
sum2 = decrypt(c_sum2,p)
sum3 = decrypt(c_sum3,p)
sum4 = decrypt(c_sum4,p)

carry = decrypt(c_carryout,p)


print("Val1:",val1)
print("Val2:",val2)

print("\nResults")

print("encrypted : \n")
print("Csum1 = {}".format(c_sum1))
print("Csum2 = {}".format(c_sum2))
print("c_sum3 = {}".format(c_sum3))
print("c_sum4 = {}".format(c_sum4))
print("carry out = {}".format(carry))
print("Sum:\t\t",carry,sum4,sum3,sum2,sum1)

Conclusion & Notes

I hope this post cleared things a bit more for you , now off you go to explore other unknown places .